При измерении какой-то величины (например, силы тока) мы обычно действуем в прямых единицах (амперах). Но иногда бывает более предпочтительно использовать относительную шкалу. В этом случае, наиболее часто используемой единицей измерений является децибел (дБ) - термин, зачастую приводящий в замешательство начинающих. При знании происхождения этого термина и одного простого правила, затруднения сведутся к минимуму, а значение величины, выраженной в децибелах, станет понятным.

Но сначала немного истории. Александр Грехэм Белл стал известен благодаря изобретению телефона. Но в его заслугах так же и работы по определению порога слышимости. В 1890 году он основал Ассоциацию глухих и плохо слышащих, которая действует до сих пор. А. Г. Белл был первым ученым, который количественно определил чувствительность   слуха и  установил, что слуховая восприимчивость зависит не от реального уровня мощности звуковой волны, достигающей нашего уха, а от ее логарифма.

Белл обнаружил, что порог слышимости ребенка составляет около 10*12 Вт/м2, а уровень, при котором возникают болевые ощущения - около 10 Вт/м2. Таким образом, диапазон громкости, нормально воспринимаемой человеком, составляет 13 порядков!

Исходя из полученных результатов, А.Г. Белл определил шкалу звуковой мощности от 0 до 13. Единицы громкости этой шкалы называются белами (последнее "л" от его фамилии было отброшено). Уровень звука тихого шепота составляет около 3 белов, а нормальной речи - около 6 белов.

Поскольку ощущение громкости базируется на логарифмической шкале уровня мощности, то преобразование между мощностью и громкостью по шкале Белла выглядит следующим образом:

громкость (в белах) = log(P1/P0), где РО - порог слышимости звука. Следовательно, уровень звука в 4 бела соответствует звуковой мощности, равной Десять в четвёртой степени умноженная на Р0.

Бел стал фактически стандартной единицей измерения логарифма отношения двух энергетических уровней: отношение, выраженное в белах, есть log(P1/P0), т.е. увеличение на 3 бела соответствует увеличению в 1000 раз. Если новое значение убывает, то логарифм отношения становится отрицательным. Чтобы сделать обратное преобразование необходимо 10 возвести в степень, равную белам.
Важнейшая особенность белов состоит в том, что они относятся только к отношению двух мощностей или двух энергий. Если же есть необходимость описания отношения двух амплитудных сигналов, например, напряжений, то возможно лишь опираться на отношение мощностей, ассоциированных с напряжениями.

Мощность пропорциональна квадрату напряжения или тока: U2 и I2.
Отношение двух напряжений, выраженное в белах, связано с отношением их мощностей: log(P1/P0) = 2log(V1/V0). Следовательно, отношение напряжений равно V1/V0 = 10(белы/2).

Стало достаточно общим выражать отношение в десятых долях бела или в децибелах (дБ). Отношение двух мощностей в дБ равняется 10log(P1/P0), а напряжений 10 умножить на 2log(V1/V0). Для получения отношения напряжений необходимо выполнить преобразование V1/V0 = 10(дБ/20).

Порой достаточно сложно определить, что считать амплитудной величиной, а что энергетической. Напряжение, ток, импеданс, напряженности электрического или магнитного полей и размахи любых волновых процессов считаются амплитудными величинами. Когда происходит измерение в децибелах, то вычисляется логарифм отношения квадратов этих величин. Энергия, мощность и интенсивность являются энергетическими величинами, и в отношении логарифма они используются непосредственно.

Например, 5% напряжения одной цепи передается в другую цепь. Отношение напряжений в этом случае равно 0,05. Для измерения в децибелах необходимо взять логарифм отношения напряжений, умножить его на 2, чтобы получить отношение в белах, а затем умножить на 10 для получения отношения в дБ: 20log(0,05) = (-26) дБ связи между сигналами.

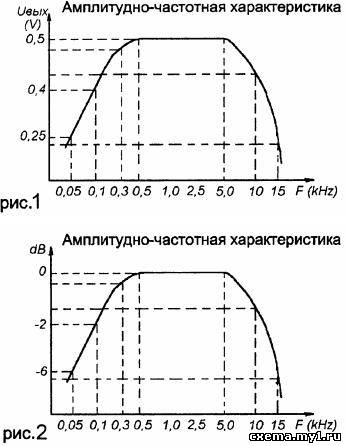
В качестве примера можно посмотреть АЧХ усилителя НЧ, выраженное в децибелах и в величинах переменного напряжения. На графике рис.1 представлена зависимость для некоторого усилителя НЧ напряжения на его выходе от частоты при постоянном уровне входного сигнала, равного 0.02V. Вроде бы все ясно, но в справочниках и «даташитах» обычно приводятся значения по оси «Y» в децибелах. В таком случае децибелы выражают отношение фактического выходного уровня на данной частоте к какому то исходному уровню, обычно полученному на частоте 1000 Гц.



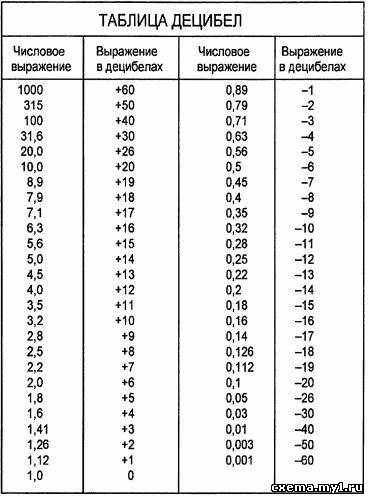
Здесь приводится таблица децибел, по которой можно, не прибегая к сложным расчетам отношение перевести в децибелы.

Делается это так: поскольку за исходный уровень взят уровень на частоте 1000 Гц, то есть, 0,5V, то напряжение 0,5V принимаем за 0 дб. Далее смотрим по графику на рис.1 и берем другие величины выходного напряжения и делим их на исходный уровень, то есть, на 0,5. А потом по таблице децибел находим значение, выраженное в децибелах. Например, 0,4/0,5=0,8, в таблице самое близкое значение 0,79, равное (-2 дб). Далее, 0,25/0,5=0,5. В таблице 0,5 соответствует (-6 дб).

Теперь строим график в децибелах (рис.2.). Можно определить диапазон рабочих частот нашего усилителя по уровню (-2 дб) и по уровню (-бдб). Согласно графика на рис.2 по уровню (-2дб) получается 100 Гц-12,5 кГц, а по уровню (-бдб) получается диапазон частот 50 Гц - 14 кГц.

Иванов А.